このサイトはいろいろな人が見に来ます。中には中学生や高校生もいますし、社会人であっても数学がそれほど得意ではないという人も少なくないでしょう。そこで、ときどきは小学生～高校生レベルの話題も取り上げていきたいと思います。今回は、三角形の面積の求め方についてです。

三角形の面積といえば、小学校を卒業した人であれば誰でも「底辺×高さ÷２」と答えることでしょう。ところがこの公式が使えるのは、「底辺」と「高さ」が分かっている場合に限られます。現実には、「底辺」というか１辺の長さは分かる可能性は高いかもしれませんが、「高さ」が直接分かることはあまりないのではないでしょうか？

例えば、中学校では三角形の合同条件というものを習います。

  • 3辺の長さが等しい
  • 2辺とその間の角が等しい
  • 1辺とその両端の角が等しい

三角形が合同だということは面積も等しいはずですから、この合同条件に関する情報が得られれば、その三角形の面積が求められるはずです。

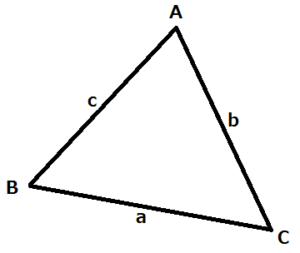
今、一般的な三角形として上のようなものを考えてみましょう。A, B, Cという3つの点からなる三角形で、それぞれの角度（内角）もA, B, Cという記号を使ってあらわすことにしましょう。そして、A, B, Cの向かい側にある辺（対辺）の長さは、それぞれa, b, cを使って表すことにしましょう。

3辺の長さから求める

3辺の長さが分かるということは、a, b, cの値が分かるということです。この3つの値だけでは「底辺×高さ÷2」という公式は使えません。このときに使うべき公式は「ヘロンの公式」です。

$$S = \sqrt{s(s – a)(s – b)(s – c)}$$

上の式中のsは次の意味です。

$$s = \frac{1}{2}(a + b + c)$$

ここまで分かれば、あとはそれぞれの文字に値を当てはめればよいだけですから簡単です。プログラムで表現することも容易にできるはずです。

3辺の長さは直接分からないけれども、3つの頂点の座標なら分かるという場合も多いことでしょう。その場合は、それぞれの座標から辺の長さを求めることができます。すなわち、「三平方の定理（ピタゴラスの定理）」を使えばよいのです。

2つの点の座標がそれぞれ (x1, y1), (x2, y2) だとすると、その2点間の距離Lは次の式で求められます。

$$L = \sqrt{(x_2 – x_1)^2 + (y_2 – y_1)^2}$$

2辺とその間の角から求める

先ほどは辺a, b, cの長さが分かっている場合でした。今度は辺a, bとその間の角Cが分かっている場合について見ていきます。

これは比較的簡単で、辺aを底辺と考えると、高さhは

$$h = b \cdot \sin C$$

あとは底辺×高さ÷2でいいので、次の式で面積を求めることができます。

$$S = \frac{1}{2} a \cdot b \cdot \sin C$$

1辺とその両端の角から求める

最後は1辺とその両端の角が分かっている場合です。これでも三角形の合同条件を満たしますから面積は求められるはずです。

これは先ほどに比べるとちょっと難しいですが、順を追ってみていけば計算式を導けるはずです。辺aとその両端の角B, Cが分かっているとしましょう。

ここで正弦定理を思い出してください。

$$\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}$$

これを使うと、辺bの長さは次のようになります。

$$b = a \cdot \frac{\sin B}{\sin A}$$

角Aは未知ですが、三角形の内角の和は180°(＝π)ですので、

$$A = π – B – C$$

であることがわかります。また、

$$\sin (π – θ) = \sin θ$$

を利用すると、sin Aは次のようになります。

$$\sin A = \sin (B + C)$$

よって、bは次の式で表すことができます。

$$b = a \cdot \frac{\sin B}{\sin (B + C)}$$

ここまでくれば、先ほどの2辺とその間の角から求める式

$$S = \frac{1}{2} a \cdot b \cdot \sin C$$

のbに代入してあげればOKです。

$$\begin{equation}
\begin{split}
S &= \frac{1}{2} a \cdot \left\{a \cdot \frac{\sin B}{\sin (B + C)} \right\} \cdot \sin C \\
&= \frac{a^2 \sin B \cdot \sin C}{2 \sin (B + C)}
\end{split}
\end{equation}$$

これで三角形の面積の求め方は一通り網羅できました。